
Introduction
What is activation function?
The typical artificial neural networks (ANN) are biologically inspired computer programs designed to function as human brain. A neuron (or artificial neuron) roughly models the neurons found in the human brain. It is a fundamental unit of processing within a neural network.
Below diagram represents the typical structure of the biological neuron –
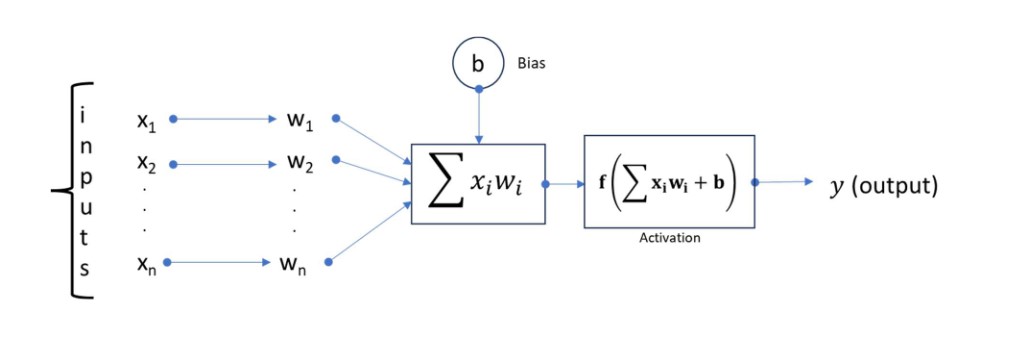
An activation function is a mathematical function (sometimes called transfer or squashing function) determines the output of a neuron based on the weighted sum of inputs from the previous layer.
The selection of activation functions affects both the capability and performance of a neural network. Technically, the activation function operates within or after the internal processing of each node in a network. Also, networks are designed to use the same activation function for all nodes in a layer.
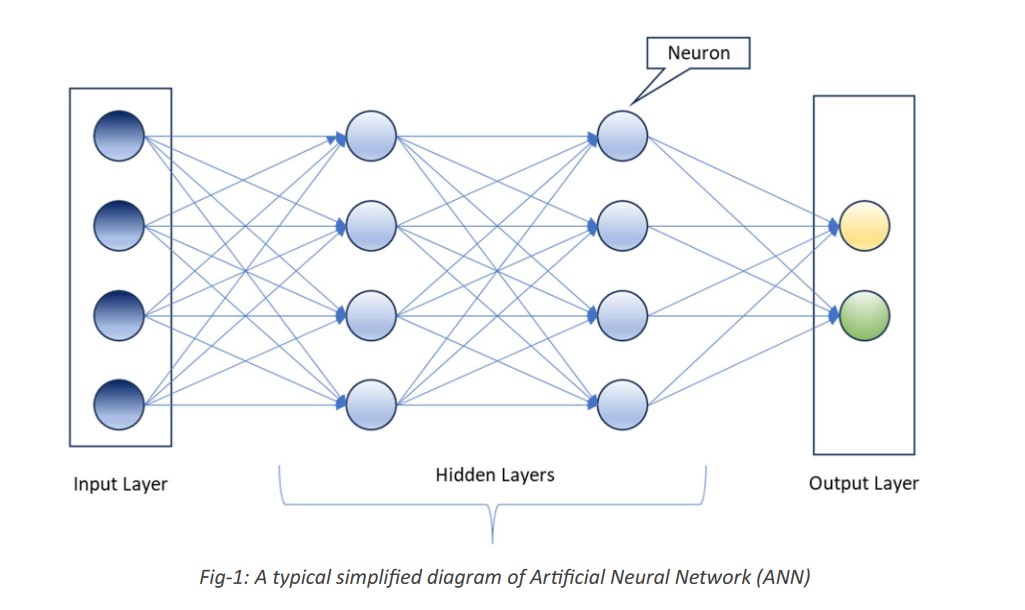
Types of activation functions
Linear Activation Functions
A linear activation function produces an output that is directly proportional to the weighted sum of its inputs.
Mathematically, it can be expressed as:
f(x) = w.x + b
On X and Y axis graph it appears as a straight line with a slope of w.
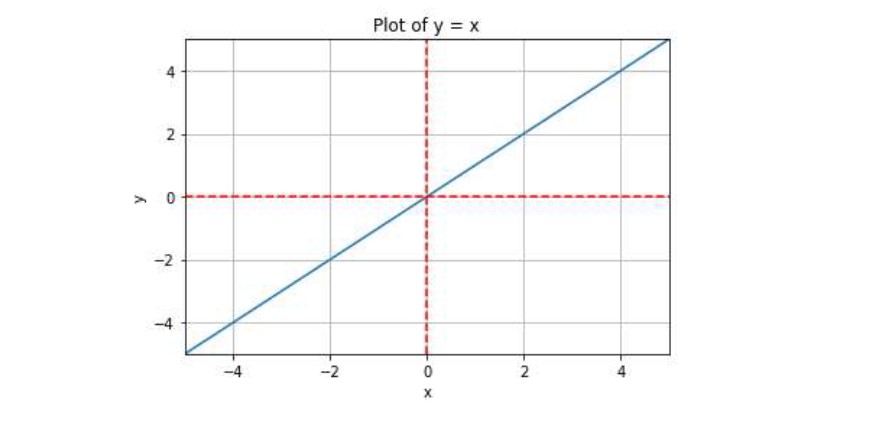
Fig-2: Plot of f(x) = x; where w = 1 and b = 0.
No matter how many layers we have, if all are linear in nature, the final activation function of last layer is nothing but just a linear function of the input of first layer. Hence, Linear activation functions are rarely used in hidden layers.
Range: (-∞, ∞)
Limitation/Issue: The differentiation of linear function is constant. Which indicates that result will no longer depends on input “x” and will not introduce any ground-breaking behavior to our algorithm.
Non-Linear Activation Functions
Non-linear activation functions are essential for modeling complex relationships and capturing non-linear patterns in data. It introduces non-linearity into a neural network’s decision-making process. By using non-linear activation functions neural networks are able to learn complex patterns and make accurate predictions.
Common Non-Linear Activation Functions
Sigmoid Activation Function
The Sigmoid function is commonly used in binary classification problems. It maps the input to a value between 0 and 1, which can be interpreted as a probability. It is useful in models that require the probability to be predicted as an output. The Sigmoid function’s smoothness allows for a gentle transition between the two extremes, making it useful for gradient-based optimization algorithms. However, the sigmoid function suffers from the vanishing gradients problem, where large input values result in small gradients, hindering the learning process.
Mathematical expression of Sigmoid function:
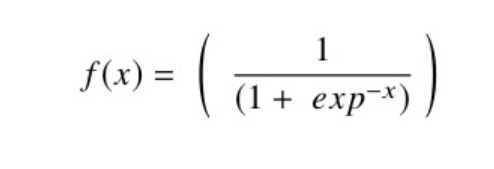
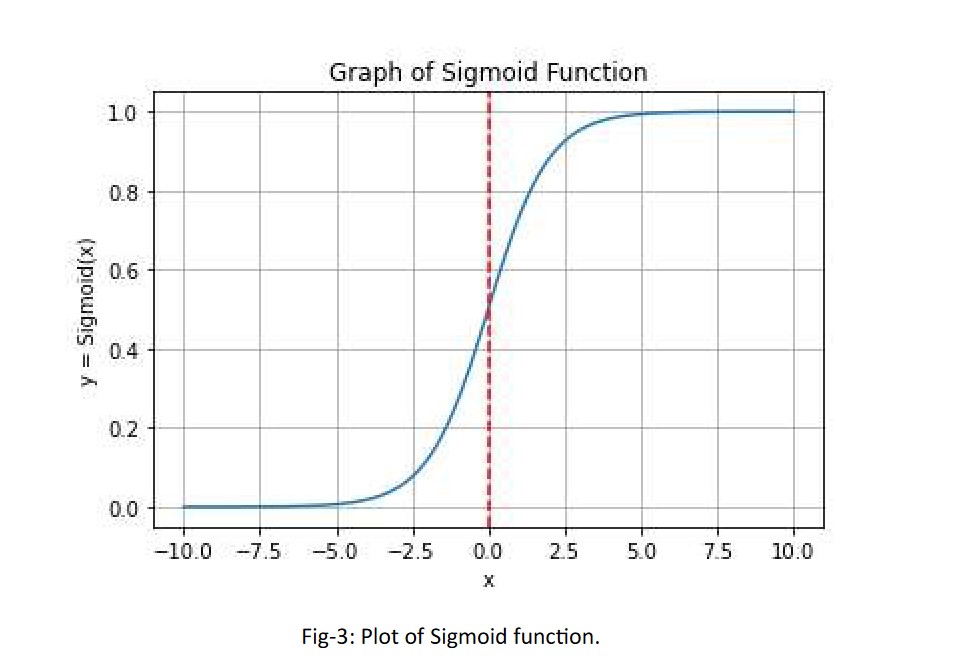
Range: (0, 1)
Limitation/Issue: Vanishing Gradient.
Hyperbolic Tangent (Tanh) activation function
The Tanh function is a smoother zero-centered function whose range lies between-1 to 1. The zero-centered property helps in capturing and propagating long-term dependencies in sequential data, such as natural language processing and time series analysis. It is preferred function compared to the sigmoid function as it gives better training performance for multi- layer neural networks. Tanh is used in Recurrent Neural Networks (RNN), Long-Short Term Memory (LSTM) Network or multi-class classification tasks.
The Tanh function can only attain a gradient of 1 when the value of the input x is 0. This makes the Tanh function produce some dead neurons during computation. The dead neuron is a condition where the activation weight, rarely used as a result of zero gradient.
Mathematical expression of Tanh function:
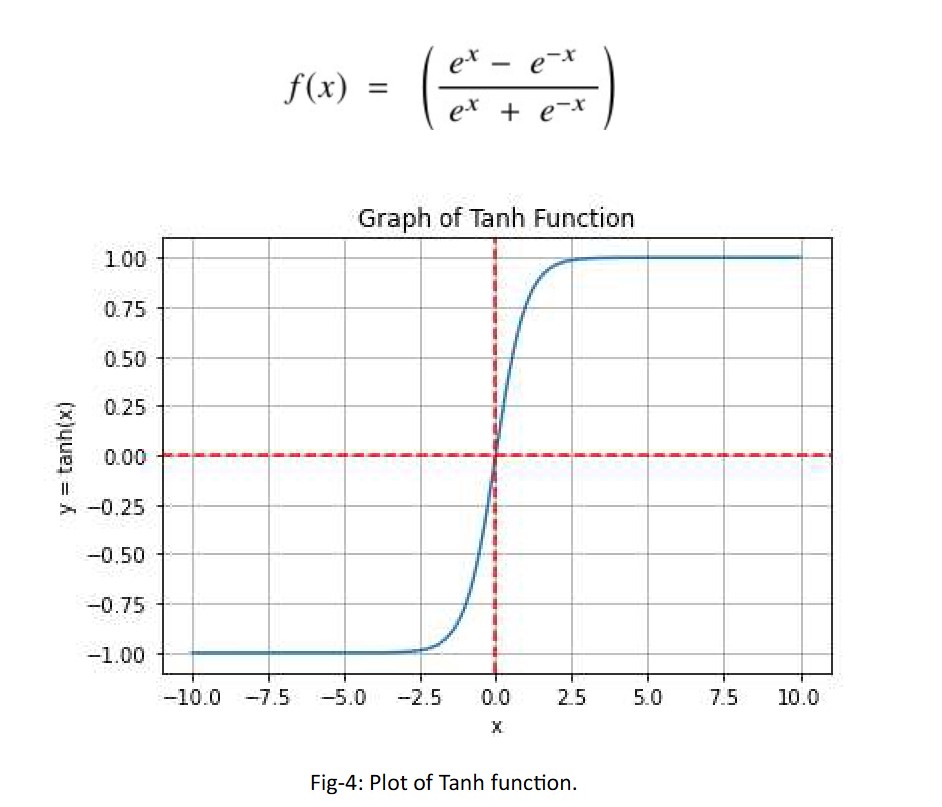
Range: (-1, 1)
Limitations/issues: The gradients tend to be smaller in the outer regions of the Tanh curve, which can slow down training.
ReLU Activation Function
The Rectified Linear Unit (ReLU) rectifies the values of the inputs less than zero thereby forcing them to zero and eliminating the vanishing gradient problem. The ReLU represents a nearly linear function and therefore preserves the properties of linear models that made them easy to optimize, with gradient-descent methods. It offers the better performance and generalization in deep learning compared to the Sigmoid and tanh activation functions.
Mathematical expression of ReLU function:
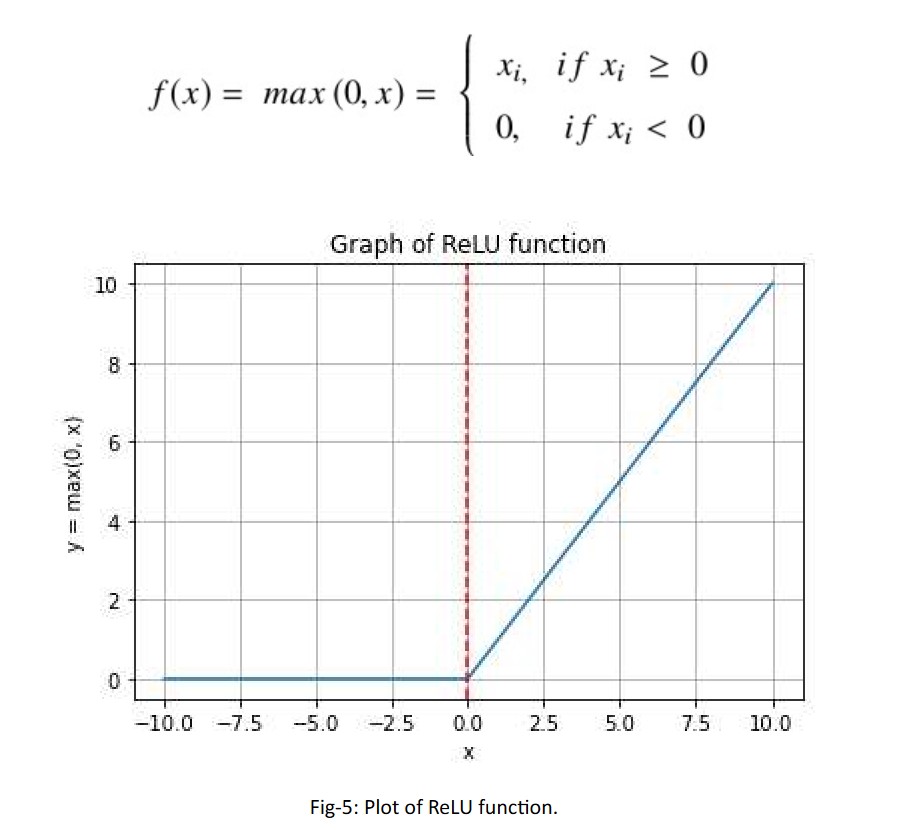
Range: [0, ∞)
Limitation/issues: Easily overfits. A large number of dead neurons impact the network’s capacity to learn.
Pankaj has held diverse roles in technology and business management, with a strong focus on software development and product delivery. His accomplishments and experiences demonstrate his leadership, technical expertise, and ability to drive change within organizations.
- This author does not have any more posts.


